© Евгений Александрович Григорьев
Фундаментальные свойства
тороидальных токовых структур.
ЭКСПЕРИМЕНТ
Показано существование внешнего магнитного поля и структура внутреннего магнитного поля в тороидальных структурах с полоидальным током.
Как было показано в работе "Уравнения Максвелла", замкнутая электрическая цепь, реализующая возможность создания постоянного магнитного поля при помощи отдельного элемента тока, может быть трансформирована в тор.
Произведены численные расчеты магнитного поля (МП) тороидальных структур с полоидальным током (Рис. 1).
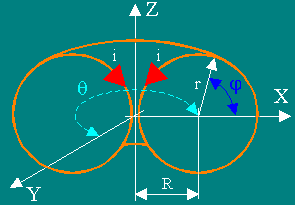
Рис. 1
Стрелками, обозначенными i , показаны векторы элементов тока. Рассматривались торы с отношением R / r ≈ 1 и R / r ≈ 2. Результаты расчетов выведены в виде графиков Кантора. Линии на графиках показывают сечение поверхностей уровня равной напряженности МП.
Направление вектора напряженности МП – перпендикулярно к плоскости изображения, так как силовые линии МП имеют исключительно азимутальную (или тангенциальную или касательную к окружности, которая лежит в плоскости XY и с центром на оси Z) составляющую.
Вначале рассчитывалось МП внутри тора.
Тор с отношением R / r ≈ 1 (Рис. 1).

Рис. 2
Тор с отношением R / r ≈ 2 (Рис. 3).
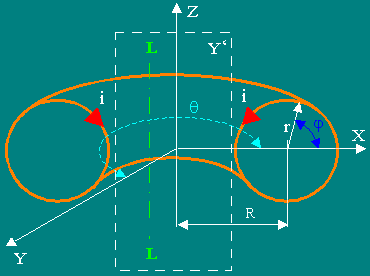
Рис. 3
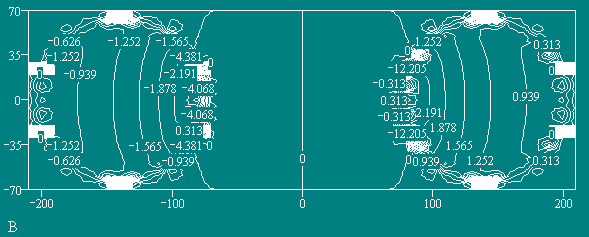
Рис. 4
На графиках (Рис.2, Рис.4) видно, что структура МП внутри тора не соответствует структуре МП бесконечного прямого проводника с током, как считалось до сих пор в классической теории электромагнетизма. Эта структура МП соответствует полю, создаваемому отдельным элементом тока, расположенным в центре тора на его главной оси и направленным вдоль этой оси. График этого МП показан на Рис. 5.
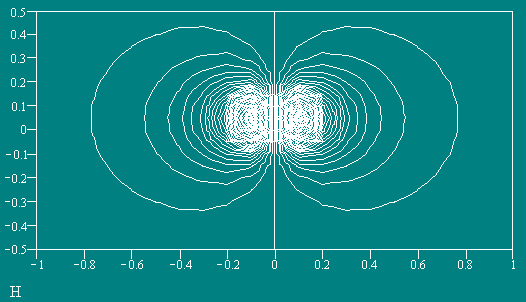
Рис. 5
Затем было рассчитано МП вне тора в плоскости XZ в ее части Y`(см. Рис.3).
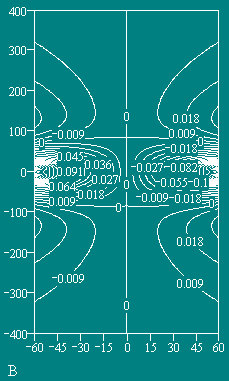
Рис. 6
Напряженность МП в плоскости Y' (y = 0) в виде графика Кантора.
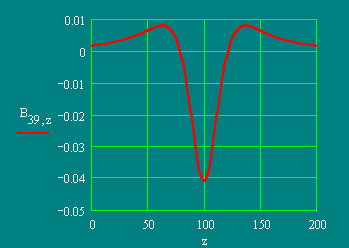
Рис. 7
Напряженность МП вдоль прямой L - L; [ у = 0, x = const, B = f(z) ].
На графике (Рис.6) видно, что внешнее МП тора существует. График на Рис.7 выявляет особенность этого МП - три максимума и два нуля. Из этого следуют два возможных варианта взаимодействия двух торов при их осевом сближении : 1) вначале возникает их отталкивание, а после преодоления потенциального барьера - притяжение; 2) вначале притяжение, а затем стабилизация на некотором расстоянии. В обоих случаях система входит в состояние с минимальным магнитным потоком (минимальной энергией) и становится устойчивой.
Предыдущие расчеты были сделаны для сплошных токовых поверхностей. Теперь сделаем расчет для тора, состоящего из отдельных прямоугольных витков с током (сегментированный тор) Рис.10. Это делается для проверки возможности воспроизведения МП сплошного тора полем сегментированных (реальных) торов. Графики – в условных единицах
Из этих двух серий графиков видно, что силовая линия МП над секционированным тором является осесимметричной окружностью с волнообразной осевой составляющей. По мере увеличения числа витков и отдаления от тора ее форма все более приближается к форме силовой линии МП, создаваемого сплошной тороидальной токовой поверхностью - идеальной окружности.
Графики, относящиеся к восьмивитковому сегментированному тору, подтверждены экспериментальными измерениями!
Эти измерения подтвердили существование подобного внешнего и расчетную структуру внутреннего МП.
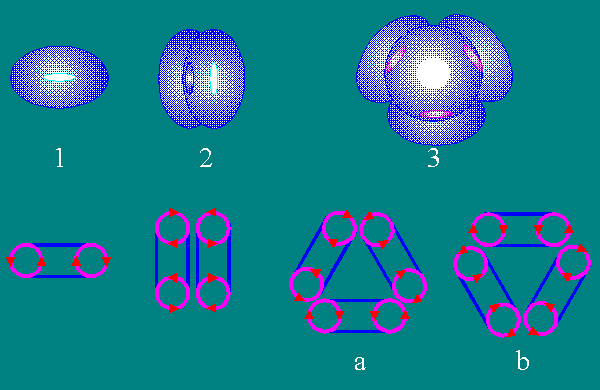
Возможные варианты взаимодействия торов.
Вполне вероятный механизм нуклеогенеза из тороидальных структур.
Расчет МП, создаваемого системой из двух соосных торов (Рис.8) показывает, что оно имеет минимум по трем координатам в центре системы (Рис.9). Все это показывает бесперспективность удержания плазмы внутренним МП в замкнутых ловушках с тороидальной конфигурацией МП типа “Токамак” и “Стелларатор” - удержание возможно только внешним МП системы из двух соосных торов произвольной конфигурации.
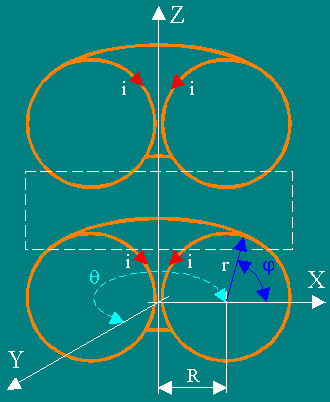
Рис. 8
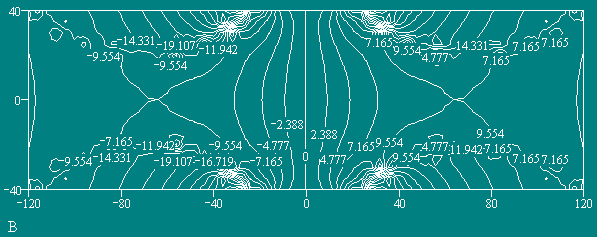
Рис. 9
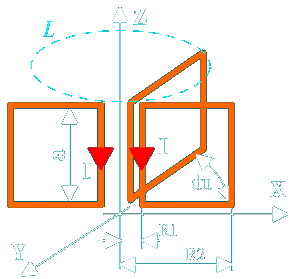
Рис. 10
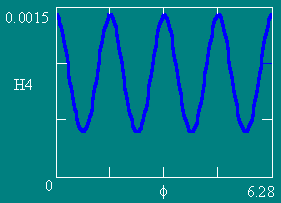
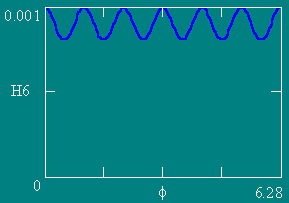
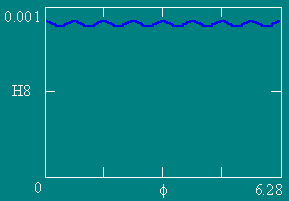
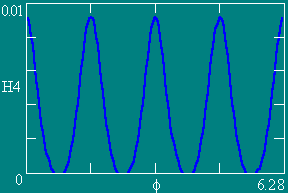
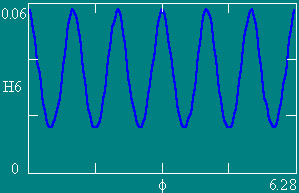
Графики зависимости напряженности МП Н по контуру L (Z = 0.1) от угла f.
Число витков NW равно 4, 6, 8 и 12 соответственно. Ампервитки постоянны.
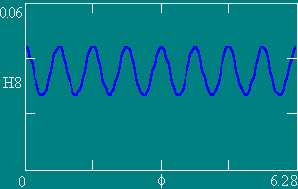
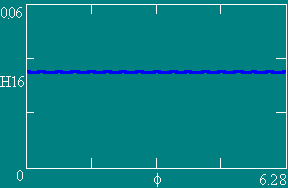
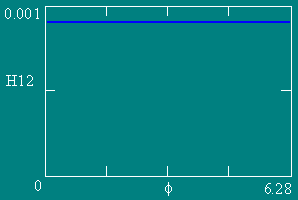
Графики зависимости напряженности МП Н по контуру L (Z = 0.05) от угла f.
Число витков NW равно 4, 6, 8 и 16 соответственно. Ампервитки постоянны.
Виток может может быть выполнен в виде обмотки.
В эксперименте, найден произвольный замкнутый контур L, не охватывающий токов (Рис. 10), по которому циркуляция вектора напряженности МП не равна нулю.
Приведены, также, расчеты конфигурации МП торов с другой геометрией: треугольная,
квадратная.
Сплошной тор Клетка Реальный тор
Версия для печати
